1. Valeur moyenne
1.1 Calcul mathématique
Soit le signal sinusoïdal La valeur moyenne
La valeur moyenne d’un signal sinusoïdal est nulle.
Le secteur est un signal sinusoïdal. Sa valeur moyenne est donc nulle. En position CC (Courant Continu) ou DC (Direct Current), un multimètre mesure la valeur moyenne.
Le secteur est un signal sinusoïdal. Sa valeur moyenne est donc nulle. En position CC (Courant Continu) ou DC (Direct Current), un multimètre mesure la valeur moyenne.
1.2 Représentation graphique
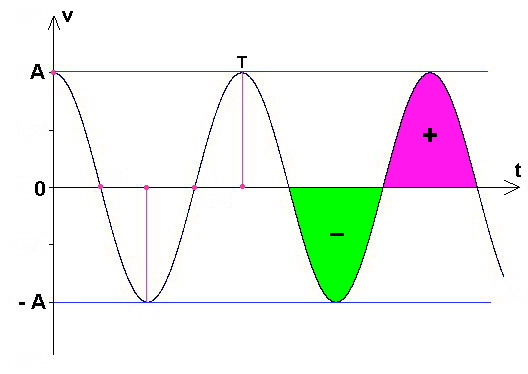
La surface située au-dessus de cet axe est considérée positive et la surface située en dessous est considérée négative.
Sur une période, les deux surfaces colorées sont d’égale valeur mais de signe contraire. Leur somme est donc nulle. On retrouve bien le résultat calculé précédemment.
2. Valeur efficace
2.1 Définition
La valeur efficace d’une tension ou d’un courant non continu est la valeur qu’aurait une tension ou un courant continu qui produirait le même effet thermique (par exemple : un échauffement identique dans une résistance).
2.2 Calcul mathématique
La valeur efficace 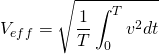 .
C’est donc la racine carrée de la valeur moyenne du carré de la grandeur considérée.
.
C’est donc la racine carrée de la valeur moyenne du carré de la grandeur considérée.En anglais, « efficace » se traduit par « RMS » : Root Mean Square.
Terminologie qui traduit parfaitement la formule précédente : racine carrée de la valeur moyenne du carré !
La valeur efficace est égale à la valeur crête divisée par racine de 2.
La valeur crête est donc égale à la valeur efficace multipliée par racine de 2.
Remarquons :
La valeur crête est donc égale à la valeur efficace multipliée par racine de 2.
En position CA (Courant Alternatif) ou AC (Alternative Current), un multimètre classique mesure la valeur efficace.
Du moins est-ce vrai pour un signal sinusoïdal et jusqu’à une certaine fréquence. Il faut donc bien connaître les caractéristiques de l’appareil de mesure que l’on utilise.
Du moins est-ce vrai pour un signal sinusoïdal et jusqu’à une certaine fréquence. Il faut donc bien connaître les caractéristiques de l’appareil de mesure que l’on utilise.
Attention : si la valeur moyenne du signal n’est pas nulle, il y a d’autres précautions à prendre…
Le secteur est un signal sinusoïdal. Sa valeur efficace vaut 230 V. Donc lorsque l’on parle du « secteur 230 V », on cite sa valeur efficace.Par conséquent, sa valeur crête est égale à 230 x 1,4142 = 325 V environ !
3. Résumé
Signal sinusoïdal :
