Signal périodique, signal sinusoïdal | Apprendre à réparer un ancien poste de radio à lampes

1. Signal périodique

On représente souvent un signal électrique au moyen d’un graphe à deux axes :
- un axe horizontal : le temps qui s’écoule,
- un axe vertical : l’amplitude du signal, par exemple en volts pour une tension.
Chaque point du graphe donne donc l’amplitude du signal $v$ à un temps $t$ donné.

Un signal périodique est un signal qui se répète identiquement à lui-même au bout d’un certain temps $T$ appelé « période ».

$\displaystyle \frac{1}{T}$ est le nombre de fois où il y a le temps $T$ en 1 seconde.
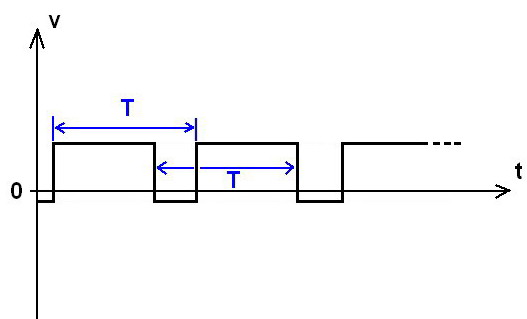
C’est « la fréquence » $F$ du signal.
Cette fréquence s’exprime en hertz (Hz). Autrefois on utilisait le terme « cycles par seconde » et même « cycles » tout simplement.

Donc 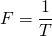$\displaystyle F=\frac{1}{T}$ et par conséquent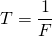 $\displaystyle T=\frac{1}{F}$

2. Signal sinusoïdal

2.1 Définition

Un signal sinusoïdal est un signal ayant la forme… d’une sinusoïde !
Il s’agit donc d’un signal périodique.

2.2 Représentation graphique

Ce n’est qu’un exemple. Ici, le signal sinusoïdal se développe autour de 0 volt. Il est tantôt positif, tantôt négatif : on dit dans ce cas particulier qu’il s’agit « d’un signal alternatif » donc ici encore, un signal alternatif sinusoïdal.

Ce signal évolue entre deux valeurs extrêmes : $A$ et $-A$ que l’on note souvent $\hat{A}$ et $-\hat{A}$ .
$A$ est « la valeur crête ».
$A-(-A)=2A$ est « la valeur crête à crête ».

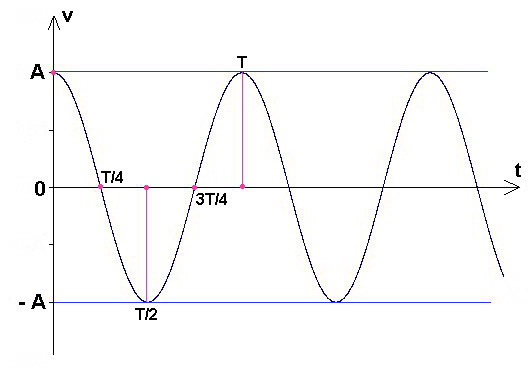
2.3 Représentation mathématique

Un signal sinusoïdal est en réalité un signal dont l’amplitude est égale aux valeurs prises par une fonction sinusoïdale du temps.
Soit $v$ ce signal sinusoïdal.
On peut donc le représenter par le sinus ou le cosinus d’un angle qui varie en fonction du temps.
Soit $\omega t$ cet angle.
$v=A\cos (\omega t)$

Pour $t=0$ , $\cos (\omega t)=1$ et donc $v=A$ , ce qui correspond bien au graphe.
Pour $t=T$ , on doit retrouver la même valeur $A$ , par définition de la période :
$v=A\cos (\omega T)=A$ .
Par conséquent $\cos (\omega T)=1$ et donc $\omega T=2\pi$ (première valeur non nulle des différentes solutions possibles).
D’où $\displaystyle \omega \ =\frac{2\pi }{T}=2\pi F$ .

$\omega$ est « la pulsation ». Elle s’exprime en radians par seconde.
Le radian est une unité d’angle : $2\pi$ radians valent 360 degrés.

Voici un tableau donnant la valeur de $v$ pour certaines valeurs bien particulières du
temps $t$ :

$t$	$\displaystyle \omega t=\frac{2\pi }{T}t$	$\displaystyle \cos \left( \frac{2\pi }{T}t \right)=\cos (\omega t)$	$v=A\cos (\omega t)$
0	0	1	A
T/4	π/2	0	0
T/2	π	−1	−A
3T/4	3π/2	0	0
T	2π	1	A
etc.

Nous retrouvons bien les points repérés sur le graphe.

3. Généralisation

Afin de regrouper toutes les écritures possibles, on utilise la formulation suivante :
$v=A\cos (\omega t+\varphi )$ .
L’expression entre parenthèses $(\omega t+\varphi )$ est un angle : c’est « la phase ». Pour $t=0$ , cette phase est égale à $\varphi$ (« phase à l’origine »). Avec $\varphi =0$ , on retrouve la représentation mathématique décrite au paragraphe 2.3.

4. Résumé

$\displaystyle \boldsymbol{F=\frac{1}{T}}$ et $\displaystyle \boldsymbol{T=\frac{1}{F}}$

$\boldsymbol{v=A\cos (\omega t+\varphi )}$ , avec $\boldsymbol{\omega =2\pi F}$

$\boldsymbol{A}$ est « la valeur crête »

Laisser un commentaire Annuler la réponse.