Circuit oscillant série | Apprendre à réparer un ancien poste de radio à lampes

1. Constitution d’un circuit oscillant série

Un circuit oscillant est composé d’une self L et d’un condensateur C. Lorsque ces deux composants sont connectés en série, nous obtenons un circuit oscillant… série !

$L$ est l’inductance de la self L.
$C$ est la capacité du condensateur C.
$r$ est la résistance de la résistance r.

Nous considèrerons que C est un composant parfait.

La résistance $r$ représente la résistance du fil constituant la self.
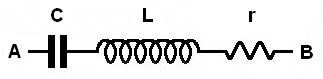
En HF, c’est plus complexe : nous étudierons un peu plus tard ce qu’est « l’effet de peau ».
En dehors de cette résistance, nous considèrerons également que L est un composant parfait.

2. Impédance d’un circuit oscillant série

Appliquons une tension sinusoïdale de pulsation $\omega$ aux bornes du circuit oscillant série.
Entre les points A et B, l’impédance $Z$ du circuit est égale à $\displaystyle r+jL\omega +\frac{1}{jC\omega }$ .
Or $\displaystyle \frac{1}{jC\omega }=\frac{j}{j}\frac{1}{jC\omega }=-j\frac{1}{C\omega }$ (car ${{j}^{2}}=-1$ ).

D’où $\displaystyle \boldsymbol{Z=r+j\left( L\omega -\frac{1}{C\omega } \right)}$ .

Cherchons la pulsation ${\omega }_{0}$ qui annulerait la partie imaginaire de ce nombre complexe $Z$ .
Cette pulsation ${\omega }_{0}$ est telle que $\displaystyle L{{\omega }_{0}}-\frac{1}{C{{\omega }_{0}}}=0$ .
Autrement dit : $\displaystyle L{{\omega }_{0}}=\frac{1}{C{{\omega }_{0}}}$ soit $\boldsymbol{LC{{\omega }_{0}}^{2}=1}$ .
Et $\displaystyle {{\omega }_{0}}=\frac{1}{\sqrt{LC}}$ .

Appelons $\ {f}_{0}$ la fréquence correspondant à ${\omega }_{0}$ :
$\ {{\omega }_{0}}=2\pi {{f}_{0}}$ .

$\displaystyle {{f}_{0}}=\frac{{{\omega }_{0}}}{2\pi }=\frac{1}{2\pi \sqrt{LC}}$

C’est la formule dite « formule de Thomson » : 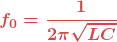$\displaystyle \boldsymbol{{{f}_{0}}=\frac{1}{2\pi \sqrt{LC}}}$ .
$\boldsymbol{{f}_{0}}$ s’appelle « la fréquence de résonance » du circuit oscillant.
À cette fréquence, l’impédance $\boldsymbol{Z}$ du circuit oscillant série n’est plus qu’une résistance pure égale à $\boldsymbol{r}$ !

3. Une autre expression de l’impédance d’un circuit oscillant série

Nous allons utiliser la fréquence dite « réduite » :
$\displays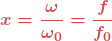tyle x=\frac{\omega }{{{\omega }_{0}}}=\frac{2\pi f}{2\pi {{f}_{0}}}=\frac{f}{{{f}_{0}}}$ .

Retenons : $\displaystyle \boldsymbol{x=\frac{\omega }{{{\omega }_{0}}}=\frac{f}{{{f}_{0}}}}$ .

Autrement dit, nous « rapportons » la fréquence $f$ à la fréquence de résonance ${f}_{0}$ .

Nous utiliserons également un autre concept : le facteur de qualité $\boldsymbol{{Q}_{s}}$ , l’indice $s$ étant là pour rappeler qu’il s’agit du facteur de qualité d’un circuit oscillant série.

Par définition :
$\displaystyle \boldsymbol{{Q}_{s}=\frac{L{{\omega }_{0}}}{r}}$ .
Comme $\displaystyle L{{\omega }_{0}}=\frac{1}{C{{\omega }_{0}}}$ , ${Q}_{s}$ peut donc également s’écrire :
$\displaystyle \boldsymbol{{{Q}_{s}}=\frac{1}{rC{{\omega }_{0}}}}$ .

Plus $r$ est faible, meilleur est le facteur de qualité. Si la self pouvait avoir une résistance $r$ nulle, elle serait parfaite et son facteur de qualité serait infini…

Reprenons notre expression de $Z$ :
$\displaystyle Z=r+j\left( L\omega -\frac{1}{C\omega } \right)$ .

Commençons par mettre $r$ en facteur :
$\displaystyle Z=r\left[ 1+j\left( \frac{L\omega }{r}-\frac{1}{rC\omega } \right) \right]$ .

Puis multiplions haut et bas par ${\omega }_{0}$ : $\displaystyle Z=r\left[ 1+j\left( \frac{L\omega }{r}\frac{{{\omega }_{0}}}{{{\omega }_{0}}}-\frac{1}{rC\omega }\frac{{{\omega }_{0}}}{{{\omega }_{0}}} \right) \right]=r\left[ 1+j\left( \frac{L{{\omega }_{0}}}{r}\frac{\omega }{{{\omega }_{0}}}-\frac{1}{rC{{\omega }_{0}}}\frac{{{\omega }_{0}}}{\omega } \right) \right]$ .

Nous y reconnaissons les 2 expressions de ${Q}_{s}$ : $\displaystyle \frac{L{{\omega }_{0}}}{r}$ et $\displaystyle \frac{1}{rC{{\omega }_{0}}}$ , d’où :
$\displaystyle Z=r\left[ 1+j\left( {{Q}_{s}}\frac{\omega }{{{\omega }_{0}}}-{{Q}_{s}}\frac{{{\omega }_{0}}}{\omega } \right) \right]$ .

Nous reconnaissons également l’expression de la fréquence réduite : $\displaystyle x=\frac{f}{{{f}_{0}}}=\frac{\omega }{{{\omega }_{0}}}$ , ce qui donne finalement :
$\displaystyle Z=r\left[ 1+j\left( {{Q}_{s}}x-\frac{{{Q}_{s}}}{x} \right) \right]$ .

L’autre expression de l’impédance $\boldsymbol{Z}$ est donc la suivante :
$\displaystyle \boldsymbol{Z=r\left[ 1+j{{Q}_{s}}\left( x-\frac{1}{x} \right) \right]}$ .

Quand $f={f}_{0}$ , $x=1$ et nous retrouvons bien $Z=r$ .

4. Impédance d’un circuit oscillant série au voisinage de la fréquence de résonance

Nous allons encore changer de variable et utiliser la dissonance $\boldsymbol{\delta}$ ainsi définie :
$\displaystyle \delta =\frac{f-{{f}_{0}}}{{{f}_{0}}}=\frac{f}{{{f}_{0}}}-1=x-1$ .

La dissonance est donc l’écart de fréquence par rapport à la fréquence de résonance rapporté à cette fréquence de résonance.

$\delta =x-1$
$x=\delta +1$

Reprenons l’expression de $Z$ obtenue au paragraphe précédent :
$\displaystyle Z=r\left[ 1+j{{Q}_{s}}\left( x-\frac{1}{x} \right) \right]=r\left[ 1+j{{Q}_{s}}\left( \frac{{{x}^{2}}-1}{x} \right) \right]$ .

Rappelons l’identité remarquable : $\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}$ et appliquons-la à $Z$ :
$\displaystyle Z=r\left[ 1+j{{Q}_{s}}\left( \frac{\left( x+1 \right)\left( x-1 \right)}{x} \right) \right]$ .

Remplaçons $x$ par sa valeur en fonction de $\delta$ :
$\displaystyle Z=r\left[ 1+j{{Q}_{s}}\left( \frac{\left( \delta +2 \right)\delta }{\delta +1} \right) \right]$ .

Au voisinage de la fréquence de résonance, $f$ est voisin de ${f}_{0}$ donc $\delta$ est proche de 0 et par conséquent négligeable devant 2 et 1 :
$\displaystyle Z\approx r\left[ 1+j{{Q}_{s}}\left( \frac{\left( 2 \right)\delta }{1} \right) \right]$ .

$\displaystyle Z\approx r\left( 1+j2{{Q}_{s}}\delta \right)$ .

Au voisinage de la fréquence de résonance, nous pouvons donc écrire, en première approximation :
$\boldsymbol{Z=r\left( 1+j2{{Q}_{s}}\delta \right)}$ .

5. Module de l’impédance d’un circuit oscillant série

5.1 Calcul

Le module de l’impédance est le module du nombre complexe 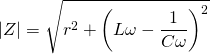$Z$ :
$\displaystyle \left| Z \right|=\sqrt{{{r}^{2}}+{{\left( L\omega -\frac{1}{C\omega } \right)}^{2}}}$ .
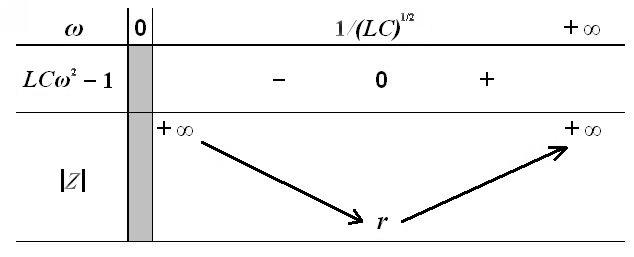
Ce module varie donc en fonction de la fréquence $f$ du signal appliqué car $\omega =2\pi f$ .
Voir l’étude de cette variation en annexe.

À la fréquence de résonance, $\displaystyle L{{\omega }_{0}}-\frac{1}{C{{\omega }_{0}}}=0$ .

Ce module est alors égal à $\sqrt{{{r}^{2}}}$ c’est-à-dire $r$ . On retrouve bien le résultat précédent.
Pour toute autre fréquence, il est supérieur à $r$ (cf. le tableau de variation).

Le module de l’impédance d’un circuit oscillant série passe par un minimum égal à $\boldsymbol{r}$ à sa fréquence de résonance.

5.2 Application numérique

$L$ = 10,286 mH

$C$ = 171 pF

$r$ = 70 Ω

Traçons la courbe de $\left| Z \right|$ en fonction de la fréquence $f$ en sachant que $\displaystyle f=\frac{\omega }{2\pi }$ :

graphe du module de l’impédance en fonction de la fréquence

Calculons la fréquence de résonance :
$\displaystyle {{f}_{0}}=\frac{1}{2\pi \sqrt{LC}} =$ 120 kHz.

À cette fréquence, $\left| Z \right|$ est bien à sa valeur minimale et cette valeur est bien égale à $r$ soit 70 Ω.

Voici le même graphe, au voisinage de la fréquence de résonance, 120 kHz :

graphe du module de l’impédance en fonction de la fréquence au voisinage de la fréquence de résonance

Au contraire, lorsqu’il sera nécessaire de représenter ce graphe sur une plage de fréquences très étendue, nous utiliserons une échelle horizontale logarithmique :
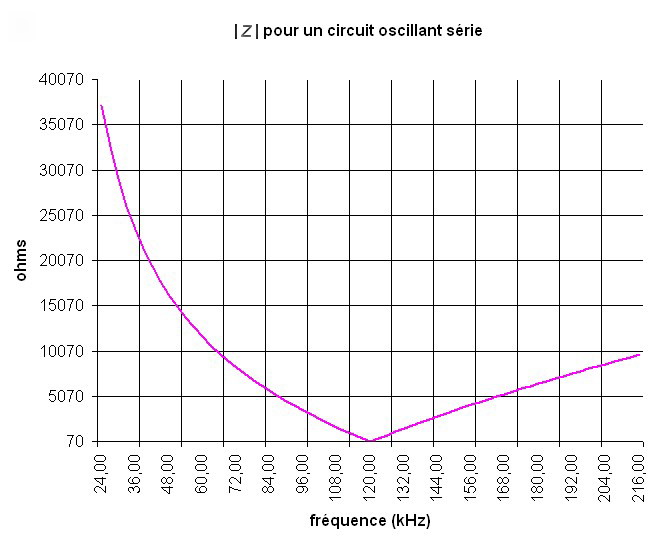
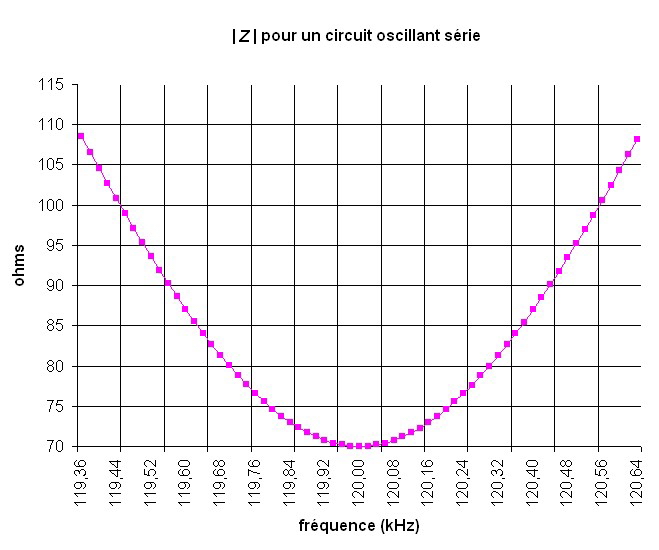
0,1 - 1 - 10 - 100 - 1000 - 10000 Hz, etc.

6. Bande passante d’un circuit oscillant série

6.1 Calcul

Nous avons vu que le module de l’impédance d’un circuit oscillant série passait par un minimum à sa fréquence de résonance. C’est même là sa caractéristique fondamentale.
Un circuit oscillant série opposera donc une faible « résistance » au passage d’un signal qui aurait cette fréquence.
Autrement dit, il privilégie ce signal. Il a donc une propriété de sélection : c’est un circuit sélectif.

Mais quid des signaux dont les fréquences seraient différentes ?
Nous allons rechercher les fréquences éventuelles où le module de l’impédance vaudrait 1,4 fois sa valeur minimale $r$ .
Ou plus exactement $\sqrt{2}$ fois ! Autrement dit, les fréquences pour lesquelles le module de l’impédance vaudrait $r \sqrt{2}$ .

Supposons ces fréquences, si elles existent, assez proches de la fréquence de résonance.
Nous pourrons donc utiliser la formule élaborée au paragraphe 4 :
$Z=r\left( 1+j2{{Q}_{s}}\delta \right)=r+j2{{Q}_{s}}\delta r$ .
${{\left| Z \right|}^{2}}={{r}^{2}}+{{\left( 2{{Q}_{s}}\delta r \right)}^{2}}={{r}^{2}}+{{\left( 2{{Q}_{s}}\delta \right)}^{2}}{{r}^{2}}$

Pour notre recherche, ${{\left| Z \right|}^{2}}={{\left( r\sqrt{2} \right)}^{2}}=2{{r}^{2}}$ .
Nous obtenons donc la condition suivante :
${{r}^{2}}+{{\left( 2{{Q}_{s}}\delta \right)}^{2}}{{r}^{2}}=2{{r}^{2}}$ .

Simplifions par ${r}^{2}$ :
$1+{{\left( 2{{Q}_{s}}\delta \right)}^{2}}=2$ soit ${{\left( 2{{Q}_{s}}\delta \right)}^{2}}=1$ ou encore $2{{Q}_{s}}\delta =\pm 1$ .

$\displaystyle \delta =\pm \frac{1}{2{{Q}_{s}}}=\frac{f-{{f}_{0}}}{{{f}_{0}}}$ (par définition de $\delta$ )
$\displaystyle f-{{f}_{0}}=\pm \frac{{{f}_{0}}}{2{{Q}_{s}}}$

Soit finalement :
$\displaystyle f={{f}_{0}}\pm \frac{{{f}_{0}}}{2{{Q}_{s}}}$ .

Il existe donc deux fréquences pour lesquelles le module de l’impédance vaut la valeur recherchée $r \sqrt{2}$ .
Elles sont symétriques par rapport à la fréquence de résonance.

La « distance » entre ces deux fréquences définit la « bande passante » $\Delta f$ :
$\displaystyle \Delta f=\left( {{f}_{0}}+\frac{{{f}_{0}}}{2{{Q}_{s}}} \right)-\left( {{f}_{0}}-\frac{{{f}_{0}}}{2{{Q}_{s}}} \right)=2\frac{{{f}_{0}}}{2{{Q}_{s}}}=\frac{{{f}_{0}}}{{{Q}_{s}}}$ .

La bande passante $\displaystyle \boldsymbol{\Delta f}$ est donc égale à $\displaystyle \boldsymbol{\frac{{{f}_{0}}}{{{Q}_{s}}}}$ .

Cette bande passante définit la largeur de bande à l’intérieur de laquelle le module de l’impédance d’un circuit oscillant série est compris entre $r$ et $r \sqrt{2}$ .

Plus le facteur de qualité du circuit oscillant est élevé, plus la bande passante est étroite.

6.2 Application numérique

Reprenons notre exemple :
$L$ = 10,286 mH

$r$ = 70 Ω

${f}_{0}$ = 120 kHz.

Calculons le facteur de qualité et la bande passante :

$\displaystyle {{Q}_{s}}=\frac{L{{\omega }_{0}}}{r}=\frac{L2\pi {{f}_{0}}}{r}=$ 110,8

$\displaystyle \Delta f=\frac{{{f}_{0}}}{{{Q}_{s}}}=$ 1,08 kHz.

La bande passante est centrée sur ${f}_{0}$ .
La fréquence basse est donc égale à 120 – 1,08 / 2 soit 119,46 kHz.
Et la fréquence haute : 120 + 1,08 / 2 soit 120,54 kHz.

Vérifions : 120,54 – 119,46 = 1,08 kHz.
Calculons aussi la dissonance $\delta$ à ces deux fréquences :
$\displaystyle \delta =\frac{f-{{f}_{0}}}{{{f}_{0}}}=\pm 0,0045$ .

Nous avions supposé les fréquences recherchées assez proches de la fréquence de résonance : notre hypothèse est bien vérifiée et l’utilisation de la formule simplifiée de l’impédance est ici parfaitement justifiée.
En effet, $\delta$ est proche de 0 et par conséquent négligeable devant 2 et 1 (cf. le paragraphe 4).

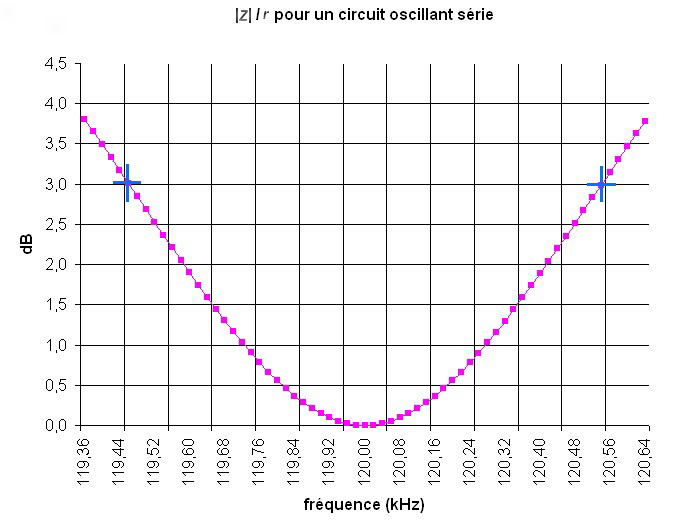
Sur le graphe ci-dessous, lorsque le module de l’impédance vaut $r\sqrt{2}$ soit 99 ohms, nous retrouvons bien les valeurs particulières de ces deux fréquences :

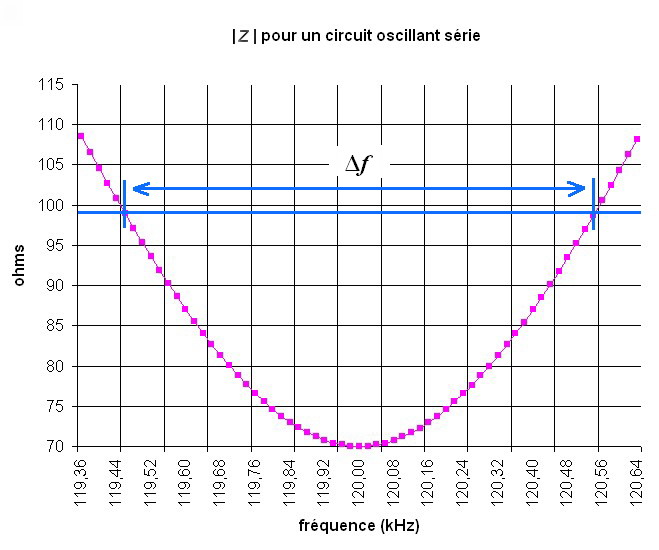
7. Décibels

7.1 Calcul

Reprenons la formule de $Z$ au voisinage de la fréquence de résonance :
$Z=r\left( 1+j2{{Q}_{s}}\delta \right)=r+jr2{{Q}_{s}}\delta$ .

$\left| Z \right|=\sqrt{{{r}^{2}}+{{\left( r2{{Q}_{s}}\delta \right)}^{2}}}=\sqrt{{{r}^{2}}\left[ 1+{{\left( 2{{Q}_{s}}\delta \right)}^{2}} \right]}=r\sqrt{1+{{\left( 2{{Q}_{s}}\delta \right)}^{2}}}$

$\displaystyle \frac{\left| Z \right|}{r}=\sqrt{1+{{\left( 2{{Q}_{s}}\delta \right)}^{2}}}$

$\displaystyle \boldsymbol{\frac{\left| Z \right|}{r}}$ est le module réduit de l’impédance : le module rapporté à $r$ , sa valeur à la fréquence de résonance.

Nous avons vu que pour déterminer la bande passante, il fallait rechercher les fréquences où le module de l’impédance valait $r\sqrt{2}$ .
Calculons le module réduit de l’impédance à ces fréquences :
$\displaystyle \frac{\left| Z \right|}{r}=\frac{r\sqrt{2}}{r}=\sqrt{2}$ .

Il est d’usage de faire le graphe de $\displaystyle \boldsymbol{20\log \left( \frac{\left| Z \right|}{r} \right)}$ plutôt que celui de $\displaystyle \boldsymbol{\frac{\left| Z \right|}{r}}$ et de noter le résultat correspondant en « décibels », « dB » en abrégé.

Remarquons que le décibel n’est pas une unité puisque le module réduit de l’impédance n’a pas de dimension : ce sont des ohms divisés par des ohms.

Aux extrémités de la bande passante :
$\displaystyle 20\log \left( \frac{\left| Z \right|}{r} \right)=20\log \sqrt{2}=20\log {{2}^{{1}/{2}\;}}$ .

Rappelons que $\displaystyle \log {{a}^{b}}=b\log a$ et appliquons : $\displaystyle 20\log \left( \frac{\left| Z \right|}{r} \right)=20\log {{2}^{{1}/{2}\;}}=20\frac{1}{2}\log 2=10\log 2$ .

Or $\log 2\approx 0,3$ .

$\displaystyle 20\log \left( \frac{\left| Z \right|}{r} \right)\approx 10 \times 0,3 = 3$ dB.

Aux extrémités de la bande passante, le module réduit de l’impédance est donc égal à 3 dB. Les fréquences correspondantes sont appelées « fréquences de coupure à 3 dB ».

À la fréquence de résonance :
$\displaystyle 20\log \left( \frac{\left| Z \right|}{r} \right)=20\log \left( \frac{r}{r} \right)=20\log 1$ .

Rappelons que $\log 1=0$ .
$\displaystyle 20\log \left( \frac{\left| Z \right|}{r} \right)=0$ dB.

À la fréquence de résonance, le module réduit de l’impédance est donc égal à 0 dB.

7.2 Application numérique

Toujours avec les mêmes valeurs, voici le graphe du module réduit de l’impédance en dB en fonction de la fréquence : 0 dB à 120 kHz, la fréquence de résonance, et 3 dB aux deux fréquences de coupure.

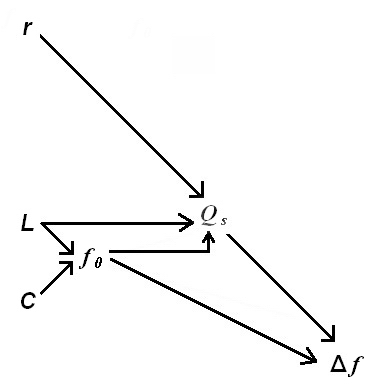
8. Synthèse pour les calculs

$L$ et $C$ donnent ${f}_{0}$ .

$r$ , $L$ et ${f}_{0}$ donnent ${Q}_{s}$ .

${f}_{0}$ et ${Q}_{s}$ donnent $\Delta f$ .

9. Résumé

$\displaystyle \boldsymbol{Z=r+j\left( L\omega -\frac{1}{C\omega } \right)}$
À la résonance, $\boldsymbol{LC{{\omega }_{0}}^{2}=1}$ et $\displaystyle \boldsymbol{{{f}_{0}}=\frac{1}{2\pi \sqrt{LC}}}$ .

À cette fréquence, le module de $\boldsymbol{Z}$ passe par un minimum égal à $\boldsymbol{r}$ .

$\displaystyle \boldsymbol{{{Q}_{s}}=\frac{L{{\omega }_{0}}}{r}}$

Plus $\boldsymbol{r}$ est petit, plus le facteur de qualité $\displaystyle \boldsymbol{{{Q}_{s}}}$ est élevé.

Au voisinage de la fréquence de résonance, $\boldsymbol{Z\approx r\left( 1+j2{{Q}_{s}}\delta \right)}$ , avec $\displaystyle \boldsymbol{\delta =\frac{f-{{f}_{0}}}{{{f}_{0}}}}$ .
Bande passante à 3 dB : $\displaystyle \boldsymbol{\Delta f=\frac{{{f}_{0}}}{{{Q}_{s}}}}$ .

Plus $\boldsymbol{{Q}_{s}}$ est élevé, plus la bande passante $\boldsymbol{\Delta f}$ est étroite.

ANNEXE

Étude de la variation du module de l’impédance d’un circuit série en fonction de la fréquence

$\displaystyle \left| Z \right|=\sqrt{{{r}^{2}}+{{\left( L\omega -\frac{1}{C\omega } \right)}^{2}}=}{{\left[ {{r}^{2}}+{{\left( L\omega -\frac{1}{C\omega } \right)}^{2}} \right]}^{{1}/{2}\;}}$

Nous ferons l’étude de la variation de ce module en fonction de $\omega$ , ce qui revient au même car $\omega=2 \pi f$ .

Dérivons $\left| Z \right|$ par rapport à $\omega$ , en nous rappelant que ${{\left( {{u}^{n}} \right)}^{\prime }}=n{u}'{{u}^{n-1}}$ :
$\displaystyle \frac{d\left| Z \right|}{d\omega }=\frac{1}{2}{{\left[ {{r}^{2}}+{{\left( L\omega -\frac{1}{C\omega } \right)}^{2}} \right]}^{{}^{-1}\!\!\diagup\!\!{}_{2}\;}}2\left( L\omega -\frac{1}{C\omega } \right)\left( L +\frac{1}{C{{\omega }^{2}}} \right)$

$\displaystyle \frac{d\left| Z \right|}{d\omega }={{\left[ {{r}^{2}}+{{\left( L\omega -\frac{1}{C\omega } \right)}^{2}} \right]}^{{}^{-1}\!\!\diagup\!\!{}_{2}\;}}\left( {{L}^{2}}\omega -\frac{L}{C\omega }+\frac{L\omega }{C{{\omega }^{2}}}-\frac{1}{{{C}^{2}}{{\omega }^{3}}} \right)$

$\displaystyle \frac{d\left| Z \right|}{d\omega }={{\left[ {{r}^{2}}+{{\left( L\omega -\frac{1}{C\omega } \right)}^{2}} \right]}^{{}^{-1}\!\!\diagup\!\!{}_{2}\;}}\frac{{{L}^{2}}{{C}^{2}}{{\omega }^{4}}-1}{{{C}^{2}}{{\omega }^{3}}}$

$\displaystyle \frac{d\left| Z \right|}{d\omega }={{\left[ {{r}^{2}}+{{\left( L\omega -\frac{1}{C\omega } \right)}^{2}} \right]}^{{}^{-1}\!\!\diagup\!\!{}_{2}\;}}\frac{\left( LC{{\omega }^{2}}+1 \right)\left( LC{{\omega }^{2}}-1 \right)}{{{C}^{2}}{{\omega }^{3}}}$

$\displaystyle \frac{d\left| Z \right|}{d\omega }$ s’annule quand $LC{{\omega }^{2}}-1=0$ donc pour $\omega ={{\omega }_{0}}$ (rappelons que $\displaystyle \omega >0$ ).

$\displaystyle {{\left[ {{r}^{2}}+{{\left( L\omega -\frac{1}{C\omega } \right)}^{2}} \right]}^{{}^{-1}\!\!\diagup\!\!{}_{2}\;}}$ est toujours positif car c’est une racine carrée.

Comme $\omega >0$ , le signe de $\displaystyle \frac{d\left| Z \right|}{d\omega }$ est celui de $LC{{\omega }^{2}}-1$ .

Voici le tableau de variation de $\left| Z \right|$ .
Pour lever le doute sur le signe de $LC{{\omega }^{2}}-1$ , il suffit de prendre $\displaystyle \omega =\frac{1}{2\sqrt{LC}}$ et $\displaystyle \omega =\frac{2}{\sqrt{LC}}$ .

tableau de variation du module de l’impédance

Laisser un commentaire Annuler la réponse.